Fatigue Life Assessment Approaches Comparison Based on Typical Welded Joint of Chassis Frame

Abstract

There are many approaches to the durability calculation that are used in engineering practice. At the same time the existing accident studies show that the leading position is still hold by fatigue failures. This means that there is still no universal approach to fatigue problem solution, and the existing approaches have their limitations. In addition, there is lack of information about the comparison between the precision of the obtained results using different approaches. In this paper different fatigue life calculation methods, like nominal stress, hot spot stress, notch stress and fracture mechanics are used to calculate the durability of T-type welded joint. The obtained results are compared with the fatigue test ones and the approaches, which give the closest results, are found.

Introduction

Time varying working loads are typical for metal constructions of chassis frames, material handling machines, ship hulls etc. According to accident studies for offshore structures [1], that took place in the North Sea, for period from 1972 to 1992, all reasons have been split into several groups according to their significance:

• fatigue 25%;
• structure collision with a ship 24%;
• dropping objects 9%;
• corrosion6%

In spite of the existence of different guides and approaches that have being used for fatigue design the significant part of failures caused by fatigue reveals the imperfection of using analysis methods. That is why the development of a new methodology is the pressing issue.

Modern fatigue design approaches are based on stress information about designing joint received from the finite element analysis of a structure. This gives the possibility of using the local stress in the probable area of the fatigue crack appearance instead of using nominal stress in the joint and broadens horizons for further enhancements.

Metal fatigue phenomena has been attracting a lot of researchers‘ interest for a long time and with the welding invention this interest even increased. The main problem was that all of researches solved particular problems (i.e. the effect of mean stress on the durability etc.) but there was no general practical approach with thorough step by step recommendations for the practicing engineers how to perform the analysis. The situation is changed during last decade when International Institute of Welding [2, 3, 4, 5], British Standard [6, 7], DNV [8, 9] have represented researches that are summarized in particular guides for the fatigue analysis with detailed description of practical utilization of the approaches, starting from mesh description and finishing with recommendations about what type of S-N curve to use.

With the aforementioned guides in the place the question of the analysis result validation has appeared. Thus, many researches have their goal to compare the fatigue experiment and analysis results [10, 11, 12, 13]. The main problem in our opinion is that in those researches only one method of the analysis is compared with the test results. But at the same time in engineering practice at least four of them are frequently used:

• nominal stress approach;
• hot spot stress approach;
• notch stress approach;
• fracture mechanics approach.

In this paper the comparison between main analytical approaches and test results for the fatigue life assessment has been done. This comparison could help to the practicing engineer to decide which approach to the durability analysis is more accurate for designing of similar joints.

For the analysis the T-type welded joint (Fig. 1) is chosen. Despite the fact that this type of connection is typical for a chassis frame, it is not covered in the researches. All the existing analysis, done for the T weld connection [10, 12, 13], have their welded gusset plate serving for stress concentration purpose only, when in the T-weld connection that is studied, the force and moment are transmitted to the main plate (crossbeam) through the gusset plate (longeron).

In the following chapters the durability of the joint is obtained using testing and different analysis approaches. The results are discussed in chapter “Discussion of the obtained results”.

Fatigue test results

The article objective is to define the approaches that give the closest result of fatigue life assessment to ones taken from fatigue test for T-type welded joint of a chassis frame [14].

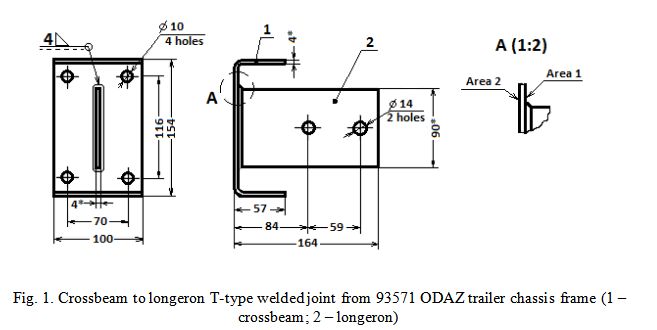
Specimens have been tested using symmetric stress cycle (R= -1). The crossbeam was fixed using 4 holes of 10 mm in diameter and the 2 forces were applied using the 2 holes of 14 mm in diameter in longeron.

The fact of the crossbeam vertical deformation amplitude increasing beyond 30 % has been used as a collapse criterion to stop the fatigue tests.

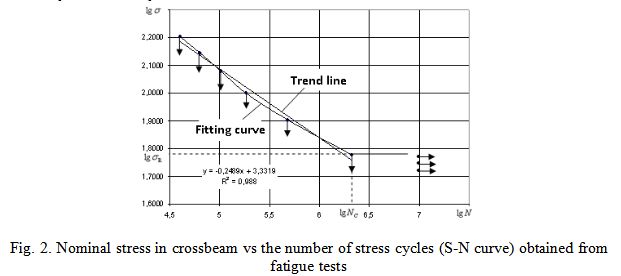
The six joints have been tested on 6 different stress levels (Table 1). The fatigue curve of Weibull type has been used

Using linear interpolation the following parameters of Eq. 1 have been found: m_w = -2.489; C_w=3.3319.

Table 1. Fatigue test results for T-weld joint crossbeam to longeron

Based on Eq. 1 the fatigue life for stress amplitude  with 50% failure probability is 425 100 cycles.

Fatigue life with failure probability of 2.3 % has been calculated using next equation:

where  d – standard deviation amount below mean value, z_P=2.3%= z_P=97.7%=2 (quantile for failure probability of 2.3%)

lg σ_N - standard deviation of lgN, 0.178, p. 20 [2] for the specimen amount n<10.

Fatigue life with failure probability of 97.7 % has been calculated using next equation:

Fig. 3. Test machine

Traditionally beam theory for nominal stress calculation is used for S-N curve. But that stress is not representative for current joint because the fracture happens not in the crossbeam outer layers but in the area of welding seam transition to the longeron (Areas 1 and 2, Fig. 1).

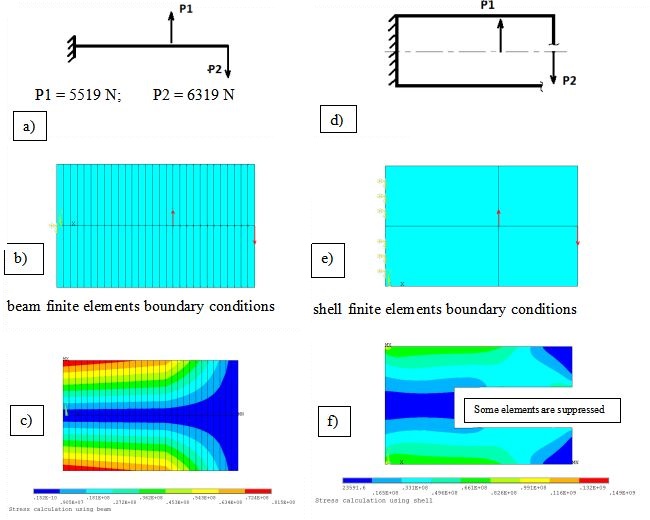
Fig. 4. Crossbeam stress calculation using finite elements of beam and shell types

Using the shell finite elements gives realistic results. Maximum stress in crossbeam for the beam finite element (Fig 3. c) is 81.5 MPa, and for shell finite element (Fig 3. f) is 159 MPa.

Moreover, stress state of crossbeam in the area of welding seam is not more uniaxial one but complex i.e. all three principal stresses have non zero magnitudes.

Nominal Stress approach

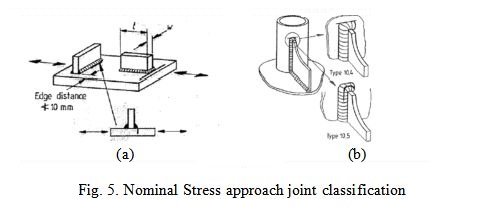
The first step of nominal stress analysis [6] is to find among the variety of joint types with boundary conditions (showed in standard) the one that corresponds to the designing joint.  But for currently calculating T-type welded connection the similar joint type does not exist. For the first look joint 5.3 (class F2, Fig. 5. a.), clause 2, Table 1, [6] could be taken, but its boundary conditions are different from analysing connection: unlike to the join from the standard the gusset plate (longeron) does not takes any load. That is why it can not be used further on. The joint on Fig 5. b can not be used for calculating either, because its boundary conditions differ from designing joint’s ones. It is also not clear stress in which element is taken for nominal (loading scheme is not shown).

Hot spot stress approach

This approach [3] allows calculating the joint fatigue life using its stress-strain state data obtained from the finite element analysis. The following joint modelling techniques are suggested to be used:

• modelling using shell finite elements. In this case welding seam is to be create in such ways:
  • model without welding seams;
  • using oblique shell elements to model welding seams;
  • using shell element with increased thickness for welding seams modelling;
• Solid modelling with volume finite elements. Idealized welding seam shape is used.

Modelling using shell elements

Model without welding seams

According to IIW Recommendations [3] welded element durability is to be calculated based on stress that acts in the weld toe. However, because of using linear elastic metal behaviour and the fact that the real weld profile is unknown on design stage, there is no possibility to use directly the stress read from welding toe. Instead, it has been proposed to use stress extrapolated value based on stress in the welding seam vicinity, so called Structural Stress.

For our case (model consists of 4 node linear shell finite elements with edge of 1.6 mm near the stress concentration point) the hot spot stress is given by:

where σ_0.4·t - stress value at the distance of 0.4·t from the weld toe (the first extrapolation point);

σ_1·t - stress value at the distance of 1·t from the weld toe (the second extrapolation point);

t – longeron thickness, 4 mm.

The finite element model of T-welded connection is shown in Fig. 6.

Fig. 6. Finite element model

The minimum thickness of the plate the approach is applicable for is 5 mm.

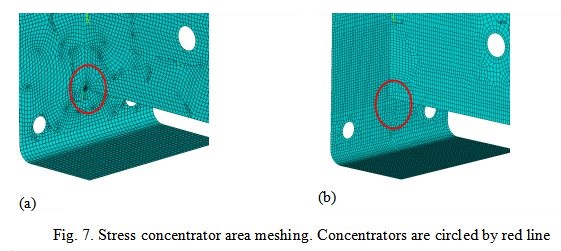
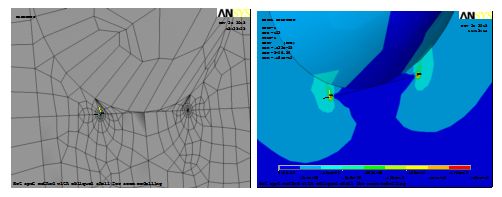
Area of the stress concentration has been meshed using two techniques (Fig. 7).

Results of finite element analysis are shown on Fig. 8; hot spot stress extrapolation calculation is put into Table 2.

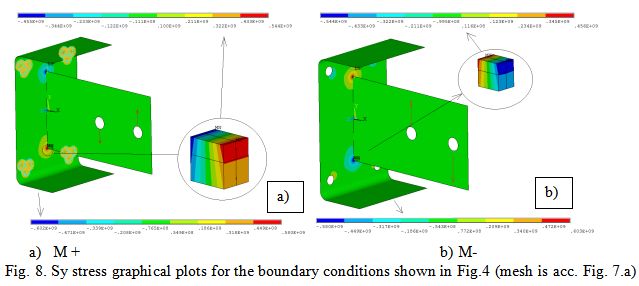
In currently overlooking standard the fatigue life assessment is based on principal stress with the biggest range during cycle. However, if the angle between this stress direction and normal to the welding seam line is more than 60 degrees, the stress perpendicular to the welding seam must be used. In our case Sy is used.

Hot spot stress approach is much easier to use in comparison with the nominal stress approach because it is based only on two S-N curves to assess the fatigue life in a “hot spots”. They are known as FAT 90 and FAT 100. The numbers that come after letters „FAT“ indicate stress level in MPa that corresponds to fatigue life for 2·10⁶ cycle durability. The general equation for these S-N curves is as follows:

where

Δσ_hs= σ_hs__max-σ_hs__min - stress range in the «hot spot», σ_hs__max - maximum hot spot stress of a cycle, σ_hs__min - minimum hot spot stress of a cycle;

m – index of power, 3.0;

С – coefficient, 2·10¹²;

N – life cycle

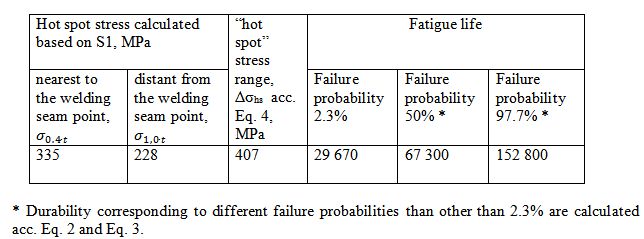
Table 2. “Hot spot” stress approximation and durability assessment

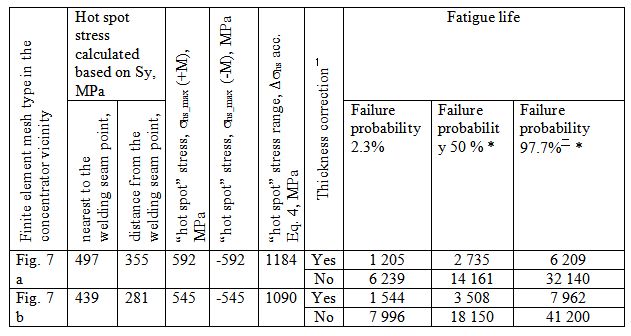
* Durability corresponding to different failure probabilities than other than 2.3% are calculated acc. Eq. 2 and Eq. 3.

Plane model with shell finite elements. Welding seam is modelled by oblique shell elements

The main concept of welding seam modelling is shown in Fig. 9 and meshed model – in Fig. 10 a).

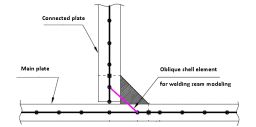
Fig. 9. Welding seam modelling with oblique shell elements

For this case first principal stress is perpendicular to the welding seam. That is why it is used for the further analysis.

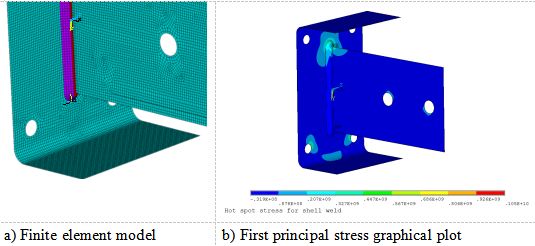
Fig. 10. Example of welding seam modelling with oblique shell elements

Table 3. “Hot spot” stress approximation and durability assessment

Solid model with volume finite elements

Solid model of the crossbeam-longeron welding connection is shown in Fig. 11. To reduce the computation time during model stress analysis only one half of the model has been created. 20 node Solid finite element with decreased integration and edge size of 4 mm is used.

The distances from the weld toe to the extrapolation points are the same (0.4·t to the first (nearest to weld) extrapolation point and 1·t to the second extrapolation point). Stress analyses result is shown in Fig. 12.

Table 4. “Hot spot” stress approximation and durability assessment

Notch Stress approach

This approach [4, 5] demands solid model creation and volume finite element mesh using. For the plate thickness less than 5 mm the Notch Radius of 0.05mm instead of 1mm has to be used, Special attention must be paid to a weld seam modelling particularly in the area where welding seam material merges to the main metal (Fig. 14 b) because the stress in this area is used for the fatigue life estimation. Only one S-N curve uses for this analysis (FAT 630) which equation takes a form of:

In addition to the weld toe modelling radius (Fig. 13) the approach specifies the welding seam geometry creation method, finite element size etc.

Fig. 13. Welding seam modelling requirements

Fig. 14. Crossbeam-longeron welding connection model for Notch Stress Analysis

Due to the high level of detail needed for welding area modelling the scope of problem increases with the growth of the joint complexity. That is why calculation time could increase from i.e. 20 minutes to several days. In this case the Sub-modelling feature is very useful. It helps to create more dense mesh and retrieve more precise solution for the smaller part of a model.

For crossbeam-longeron joint welding seam area sub-model of a fatigue crack initiation is shown in Fig 15.

Fig. 15. Crossbeam-longeron welding connection sub-model

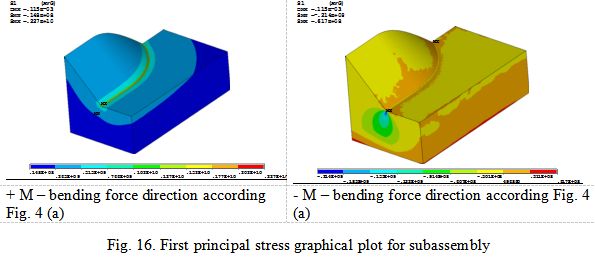
Table 5. Principal stress variation during cycle and durability assessment

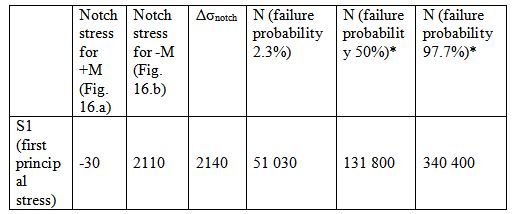
* Durability corresponding to different failure probabilities than other than 2.3% are calculated acc. Eq. 2 and Eq. 3. According [5] standard deviation of the lgN=0.206.

Fracture Mechanics based approach

The central idea of the approach [2, 3] consists in the using Paris equation for assessment of the joint fatigue stress cycles number till failure:

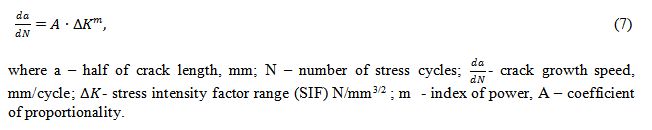
According to [7] either of two types of the crack growth relationship (Fig.17) could be used.

Using Eq. 7 the crack length – stress cycle relationship could be obtained:

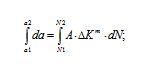
After solving integral equation Eq. 8 the stress cycle number could be defined (N=N₂-N₁) that is needed for crack growth from length 2a₁ to 2a₂.

As per fracture mechanics theory a crack starts to grow if SIF range exceeds some threshold value (), which is different for different grades. Only SIF ranges more than this threshold are considered in analysis.

The failure criterion for the fatigue testing of the crossbeam-longeron welding connection is the 30% of longeron deformation range increasing. This corresponds to the crack length of L=2a=35.5 mm.

The method of solving Eq. 8 is as follows:

• Define the SIF variation as the approximation  . To do this the models of the joint with different crack lengths are created and for each crack length the SIF is calculated (calculation results are shown in Table 6 and Table 7)
• Substitute the obtained approximation into the integral equation Eq. 8 and integrate

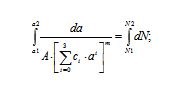
The initial limit, a₁ corresponds to SIF threshold value of the material (170   for R=-1, acc. (48 c), 8.2.3.6 [7]). Final limit, a₂=17,75 mm comes from the failure criterion during test.

As the life of crack initiation for welded joints is a small part of the total life [15], we will neglect it. The minimum crack length is defined for each case based on threshold SIF.

After analysis it became clear, that SIFs for all three modes are nonzero. Next Eq. 10 and Eq. 11 have been used to calculate the effective SIF, corresponding to the complex loading, that takes into consideration SIFs for all three different modes. Linear elastic material model has been used.

Table 6. Crack growth modelling results

As all three SIF are not equal to 0 the equivalent SIF has to be used for further analysis.

First model for equivalent SIF calculation:

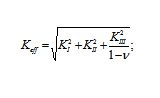
Second model for equivalent SIF calculation:

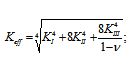
First Model for equivalent SIF calculation with one stage crack growth relationship

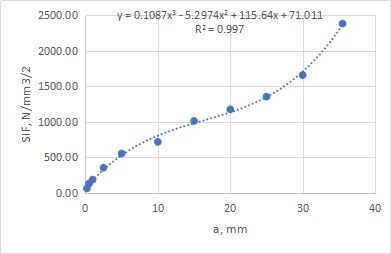
The SIF approximation is shown on the graph above as a trend line equation

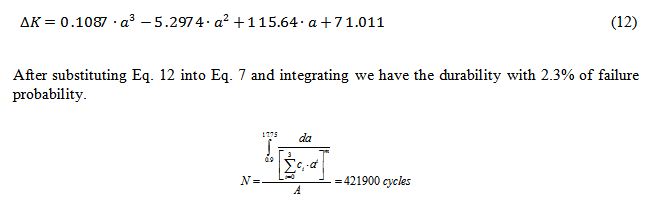
where m - index of power, 3, clause 8.3.3.5, [7],

А – coefficient of proportionality, 5.21·10^-13, clause 8.3.3.5 [7],

a₁ for this case equals to 0.9 mm.

First Model for equivalent SIF calculation with two stage crack growth relationship

Total durability would consist of durability for two stages (stage A and stage B). For the Mean Curve (Table 10 [7]) the stage A/Stage B transition point is 196, which corresponds to a=1.15 mm.

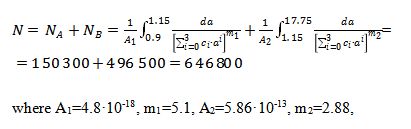
where A₁=4.8·10^-18, m₁=5.1, A₂=5.86·10^-13, m₂=2.88,

For the Mean Curve + 2SD (Table 10 [7]) The stage A/Stage B transition point is 144, which is smaller than the threshold value and that why during the Stage A the crack will not propagate.

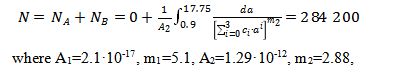
Table 7. Crack growth modelling results

Fig. 20. Approximation of SIF range vs. crack length relation (the polynomial approximation is shown above the trend line)

The SIF approximation is shown on the graph above as a trend line equation

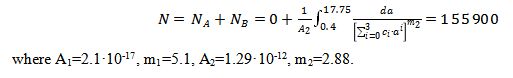
Discussion of the obtained results

• It has been found that for the case of Hot Spot stress approach analysis without weld seam modelling the local orientation of 1st principal stress near the gusset plate to main plate connection ends is not perpendicular to the welding seam and that is the reason for using stress component perpendicular to the seam. At the same time for the cases where the welding seam is modelled (both shell and solid models) the 1st principal stress is perpendicular to the welding seam. Thus, the local stress strain state in models without modelled seams does not reflect the reality and the fatigue analysis based on local stress in these areas is not correct.
• The thickness correction for 4 mm plate, applied with „Hot Spot“ stress approach, when the higher FAT class is used, gives significant overestimation of the joint durability.
• For the case when weld seam is NOT modelled the lower stress is , but for models with welding seam . As the result the stress range for the models without welding seam is approximately twice bigger than for model with seam modelled.

Conclusion

Having analysed obtained results for crossbeam – longeron welding connection and compared them with the fatigue test following conclusion has been done:

1. Fatigue life assessment based on Nominal stress approach could be utilized only if the geometry and boundary conditions (type of joint fixation and applying loads) of the analysing joint comply with the one from the existing schemes of the Codes, for which data has been originally obtained by fatigue testing. The biggest problem is that the Codes do not cover all possible types of boundary conditions. For example, in the case of crossbeam-longeron joint analysis this method could not be used because the appropriate loading scheme could not be found in the Standard.
2. The closest to the fatigue test results are given by the fracture mechanics approach based on equivalent Stress Intensity Factor calculated acc. Eq. 11 in combination with:
   3. one stage crack growth relationship (difference with test is 3.75%; the result is NOT conservative as the calculated durability is more than the test results);
   4. two stage crack growth relationship (difference with test is -16.75 %; the result is conservative as the calculated durability is less than the test results).
3. The worst correlation with the test shows the “Hot Spot” stress-based approach without the seam modelling.
4. “Notch Stress” analysis result is close to the one obtained using “Hot Spot” stress analysis.
5. Regarding to the “Notch Stress” approach its main merit is that only this method among described above could predict the durability for the cases where the crack initiates from the weld root. Thus, sometimes it is only one option for analysis.

Acknowledgement

I would like to express my gratitude to the following my colleagues from Liebherr Mining Equipment for their valuable comments to may paper: James Witfield PE, Dr. Vladimir Pokras, Michael Karge.

Special appreciation is to my teacher, Doctor of technical science, Prof. Konoplyov A. V., for his permission to use the fatigue test results he has carried out.

References  

• Review of Repairs to Offshore Structures and Pipelines, Publication 94/102 Marine Technology Directorate, UK, 1994.
• Fricke, Guideline for the fatigue design of welded joints and components XIII-1539-96/XV-845-96, 2010.
• Niemi, W. Fricke and S.J. Maddox, Fatigue Analysis of Welded Components. Designer guide to the structural hot-spot stress approach, IIW-1430-00, 2007.
• Fricke, IIW Guideline for the Assessment of Weld Root Fatigue IIW-Doc. XIII-2380r3-11/XV-1383r3-11, 2012
• Guideline for the Fatigue Assessment by Notch Stress Analysis for Welded Structures IIW-Doc. XIII-2240r2-08/XV-1289r2-08 Wolfgang Fricke, 2010
• BS 7608-1993 Fatigue design and assessment of steel structures, 1993.
• BS 7910 Guide on methods for assessing the acceptability of flaws in metallic structures, 1999.
• RP-203: Fatigue Design of Offshore Steel Structures, DNVGL-RP-0005:2014-06
• Fatigue assessment of ship structures DNVGL-CG-0129, 2015
• Baik, K. Yamada, T. Ishikawa, Fatigue Strength of Fillet Welded Joint subjected to Plate Bending, Steel Structures, 8 (2008) 163-169
• Lassen, N. Recho, Fatigue life analysis of welded structures, ISTE, 2006
• Comparison of hot spot stress evaluation methods for welded structures J-M. Lee, J-K. Seo, M-H. Kim, S-B. Shin, M-S. Han, June-Soo Park, and M. Mahendran, Inter J Nav Archit Oc Engng, (2010) 2:200~210
• Lotsberg, Fatigue design of plated structures using finite element analysis, Ships and Offshore Structures, (2006), 45-54
• General classification creation: Doctor of technical science thesis: 05.02.02/ Konoplyov A. V; Odessa National Polytechnical University. – O., 2013. – 39p. [inUkrainian] (Експериментально-розрахункові методи визначення границі витривалості деталей машин. Створення їх єдиної класифікації [Текст] : автореф. дис. ... д-ра техн. наук : 05.02.02 / Конопльов Анатолій Васильович ; Одес. нац. політехн. ун-т. - О., 2013. - 39 с. : рис.)
• Draper, Modern Metal Fatigue Analysis, Birchwood Park, Warrington : EMAS Pub, 2008.